DSA-Using-C

7. Multi-linked Lints

In a multi-linked list, each node can have n number of pointers to other nodes. A doubly linked list is a special case of multi-linked lists. However, unlike doubly linked lists, nodes in a multi linked list may or may not have inverses for each pointer. We can differentiate a doubly linked list from a multi-linked list in two ways:

• (a) A doubly linked list has exactly two pointers. One pointer points to the previous node and the other points to the next node. But a node in the multi-linked list can have any number of pointers.

• (b) In a doubly linked list, pointers are exact inverses of each other, i.e., for every pointer which points to a previous node there is a pointer which points to the next node. This is not true for a multi-linked list.

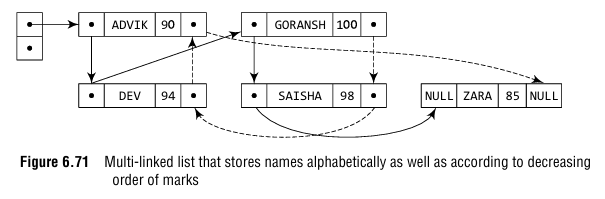
Multi-linked lists are generally used to organize multiple orders of one set of elements. For example, if we have a linked list that stores name and marks obtained by students in a class, then we can organize the nodes of the list in two ways:

• (i) Organize the nodes alphabetically (according to the name)

• (ii) Organize the nodes according to decreasing order of marks so that the information of student

who got highest marks comes before other students. Figure 6.71 shows a multi-linked list in which students’ nodes are organized by both the aforementioned ways.

A new node can be inserted in a multi-linked list in the same way as it is done for a doubly linked list.

note In multi-linked lists, we can have inverses of each pointer as in a doubly linked list. But for that we must have four pointers in a single node.

/image/list/72.png

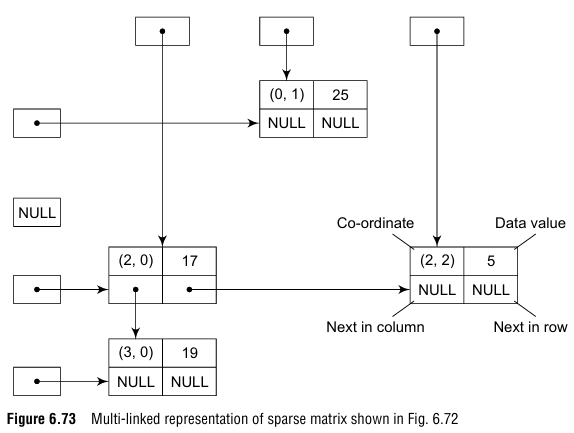
Multi-linked lists are also used to store sparse matrices. In Chapter 3 we have read about sparse matrices. Such matrices have very few non-zero values stored and most of the entries are zero. Sparse matrices are very common in engineering applications. If we use a normal array to store such matrices, we will end up wasting a lot of space. Therefore, a better solution is to represent these matrices using multi-linked lists.

The sparse matrix shown in Fig. 6.72 can be represented using a linked list for every row and column. Since a value is in exactly one row and one column, it will appear in both lists exactly once. A node in the multi-linked will have four parts. First stores the data, second stores a pointer to the next node in the row, third stores a pointer to the next node in the column, and the fourth stores the coordinates or the row and column number in which the data appears in the matrix. However, as in case of doubly linked lists, we can also have a corresponding inverse pointer for every pointer in the multi-linked list representation of a sparse matrix.

note When a non-zero value in the sparse matrix is set to zero, the corresponding node in the multi-linked list must be deleted.